Control-Flow Flattening

When to use it?

While reverse engineering a function, the control-flow graph is really important for as it provides information about the different conditions to reach the basic blocks of the function. In addition, the decompilation process relies – to some extend – on this control flow.

Let’s consider this function:

bool check_password(const char* passwd, size_t len) {
  if (len != 5) {
    return false;
  }
  if (passwd[0] == 'O') {
    if (passwd[1] == 'M') {
      if (passwd[2] == 'V') {
        if (passwd[3] == 'L') {
          if (passwd[4] == 'L') {
            return true;
          }
        }
      }
    }
  }
  return false;
}

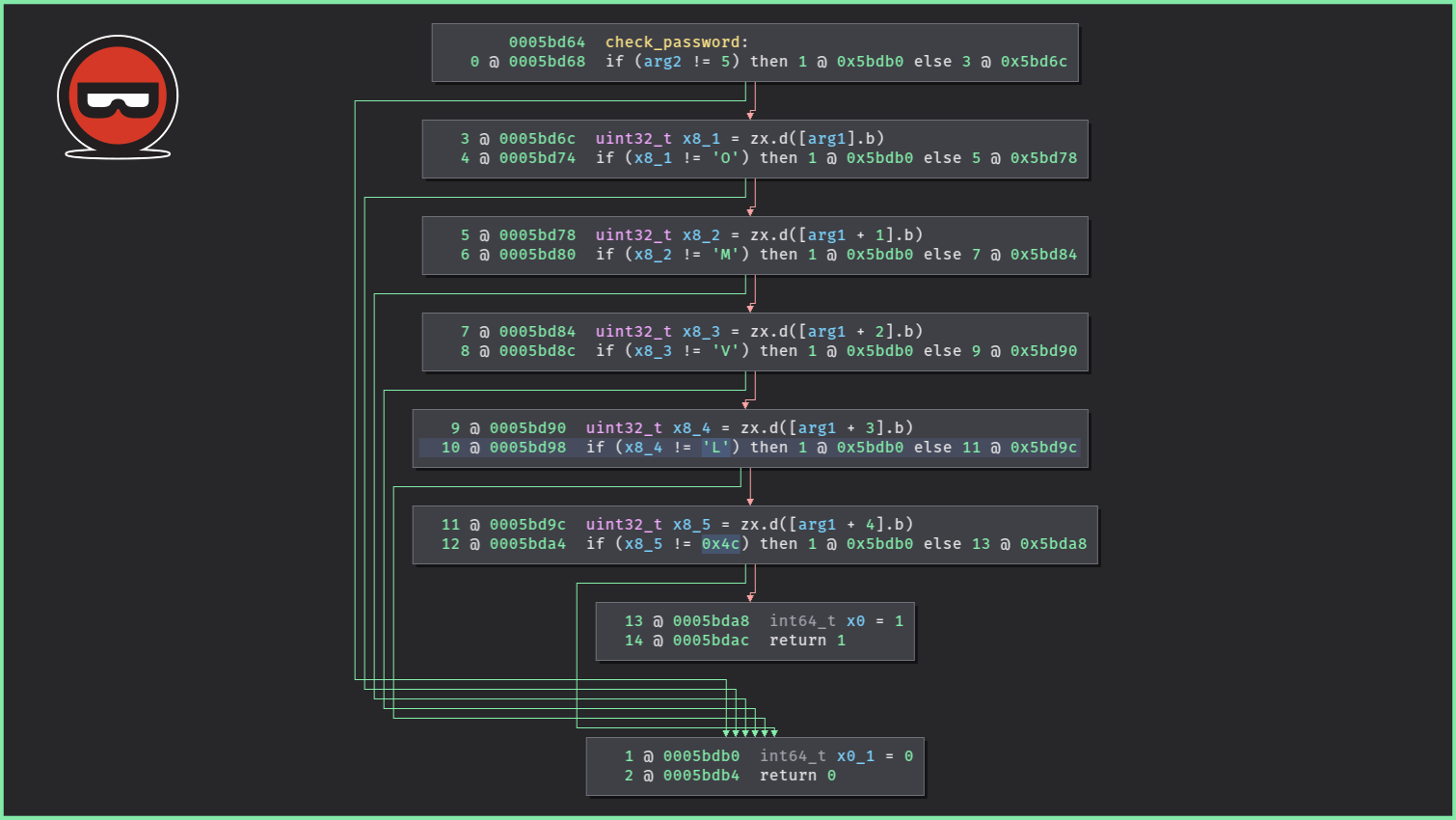
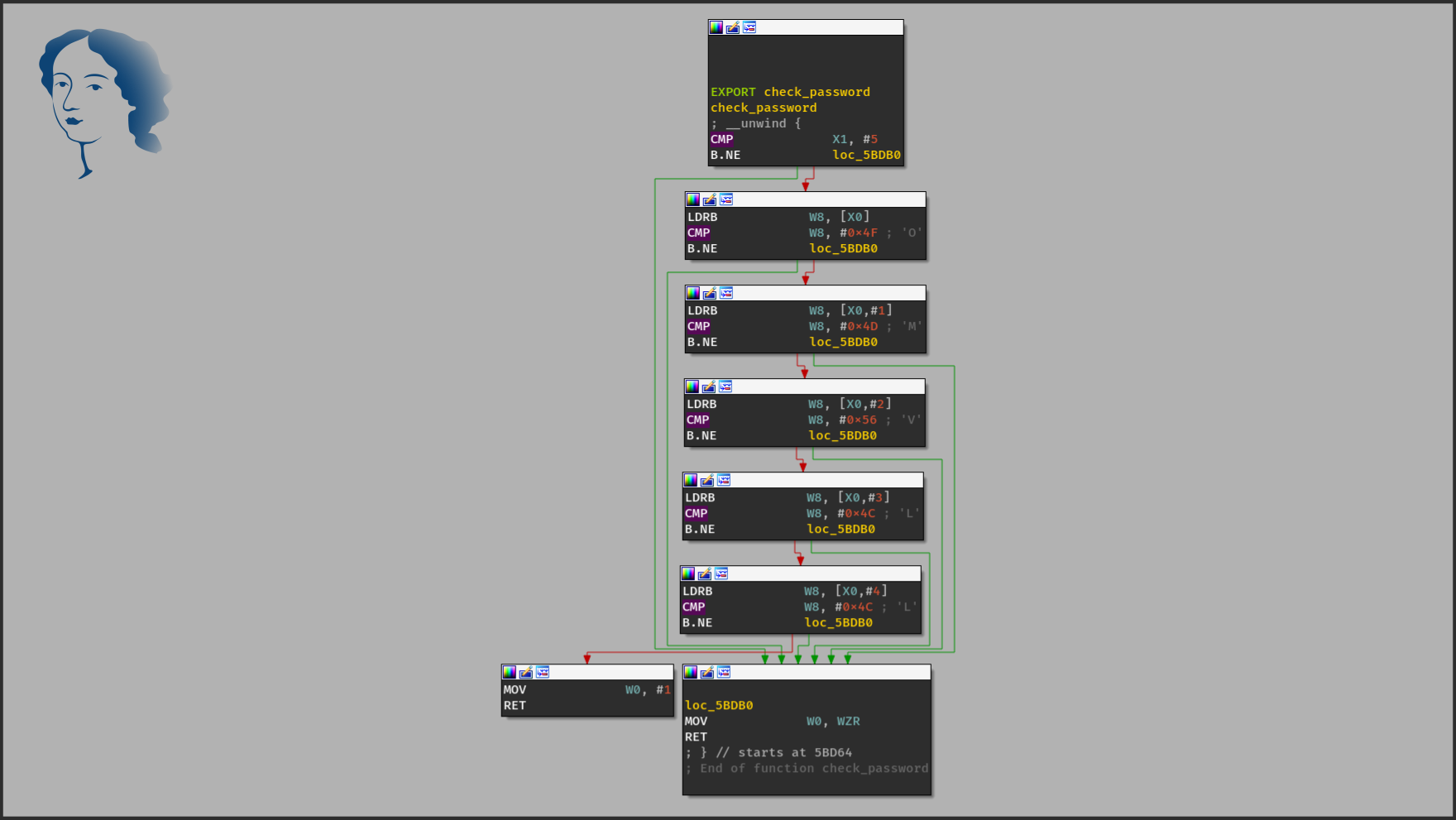
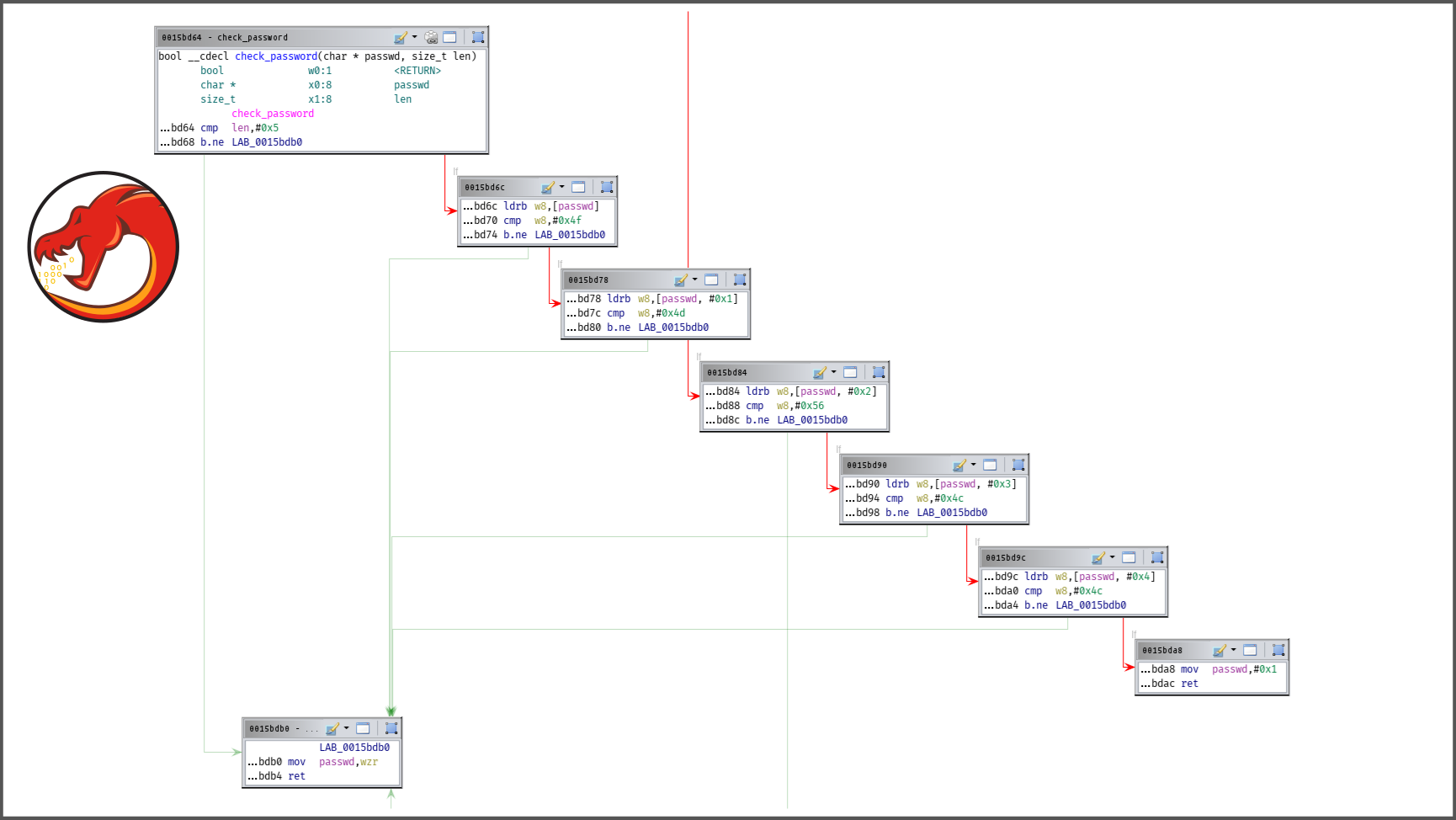
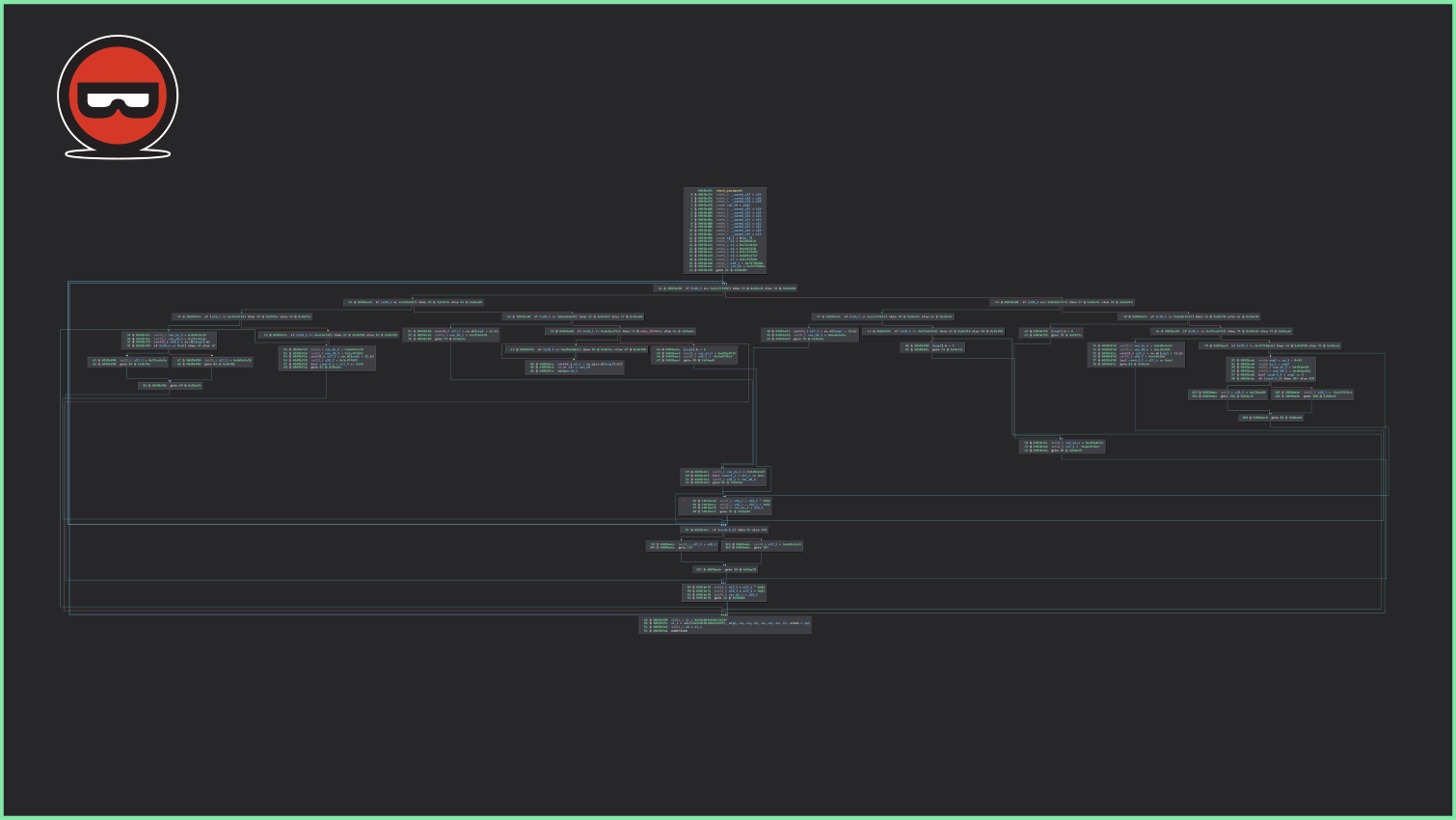
When the function is compiled, we can observe the following graphs in the reverse engineering tools:

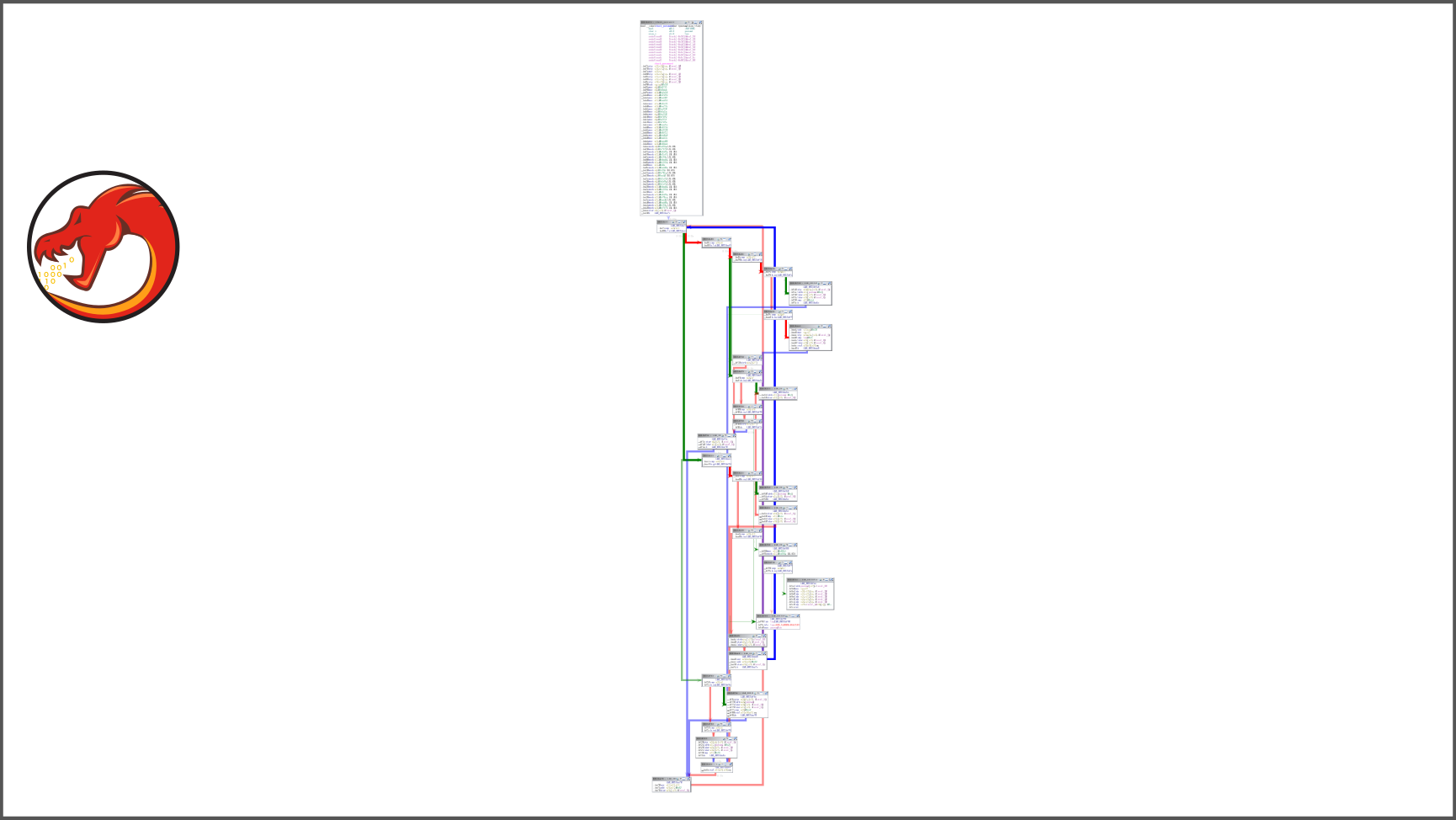
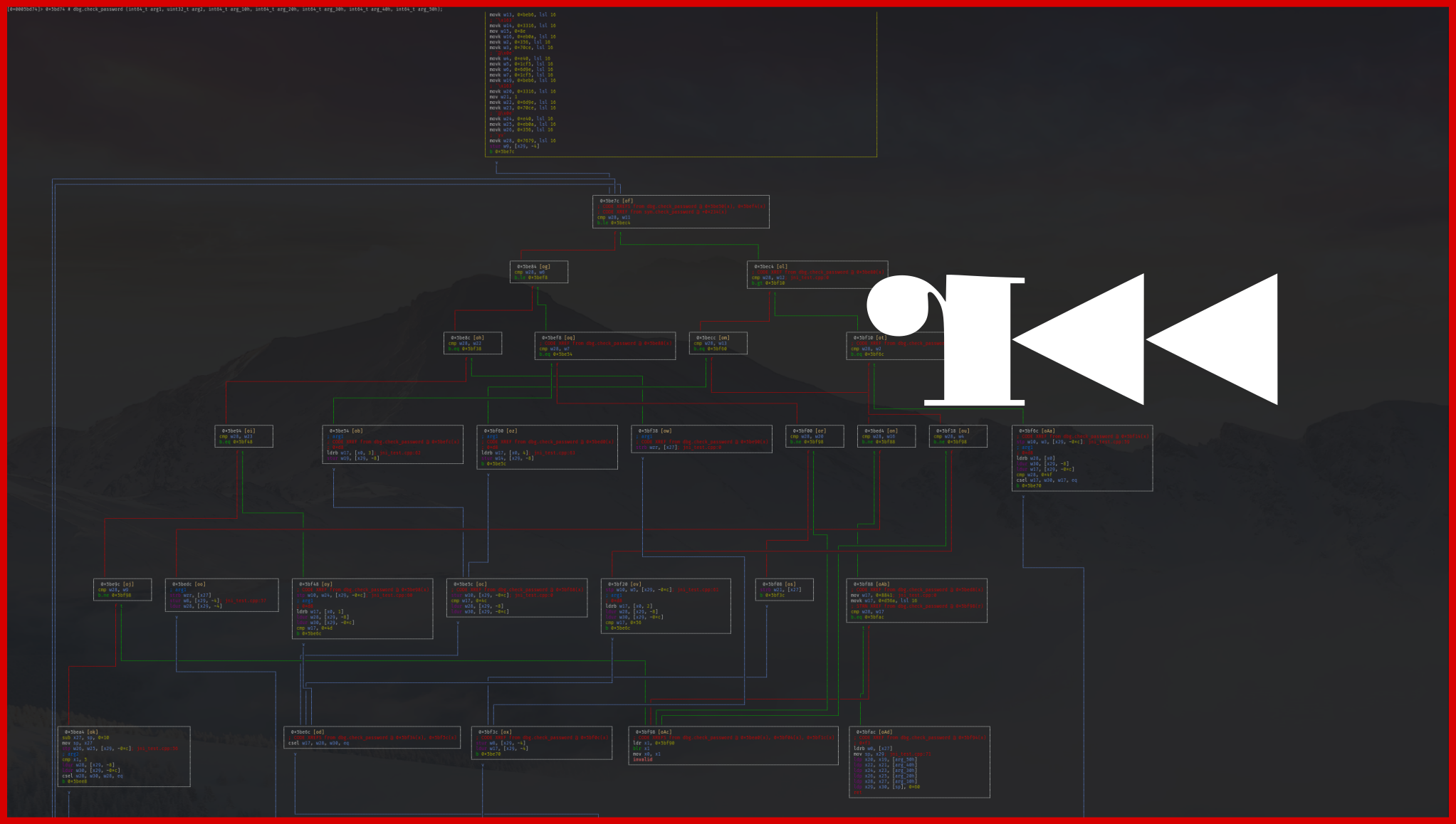
We can clearly identify both: the conditions and how the sequence of the basic block is driven. By using the control-flow flattening protection, the (basic) blocks a wrapped in a kind of switch-case:

bool check_password(const char* passwd, size_t len) {
  state_t state;
  switch (ENC(state)) {
    case 0xedf34:
      state = (len != 5) ? 0x48179 : 0xd51b;
      break;
    case 0xedf34:
      state = (passwd[0] == 'O') ? 0x48179 : 0xd51b;
      break;
    case 0xedf34:
      state = (passwd[0] == 'O') ? 0x48179 : 0xd51b;
      break;
    ...
    case XXX: return true;
    case XXX: return false;

  }
}

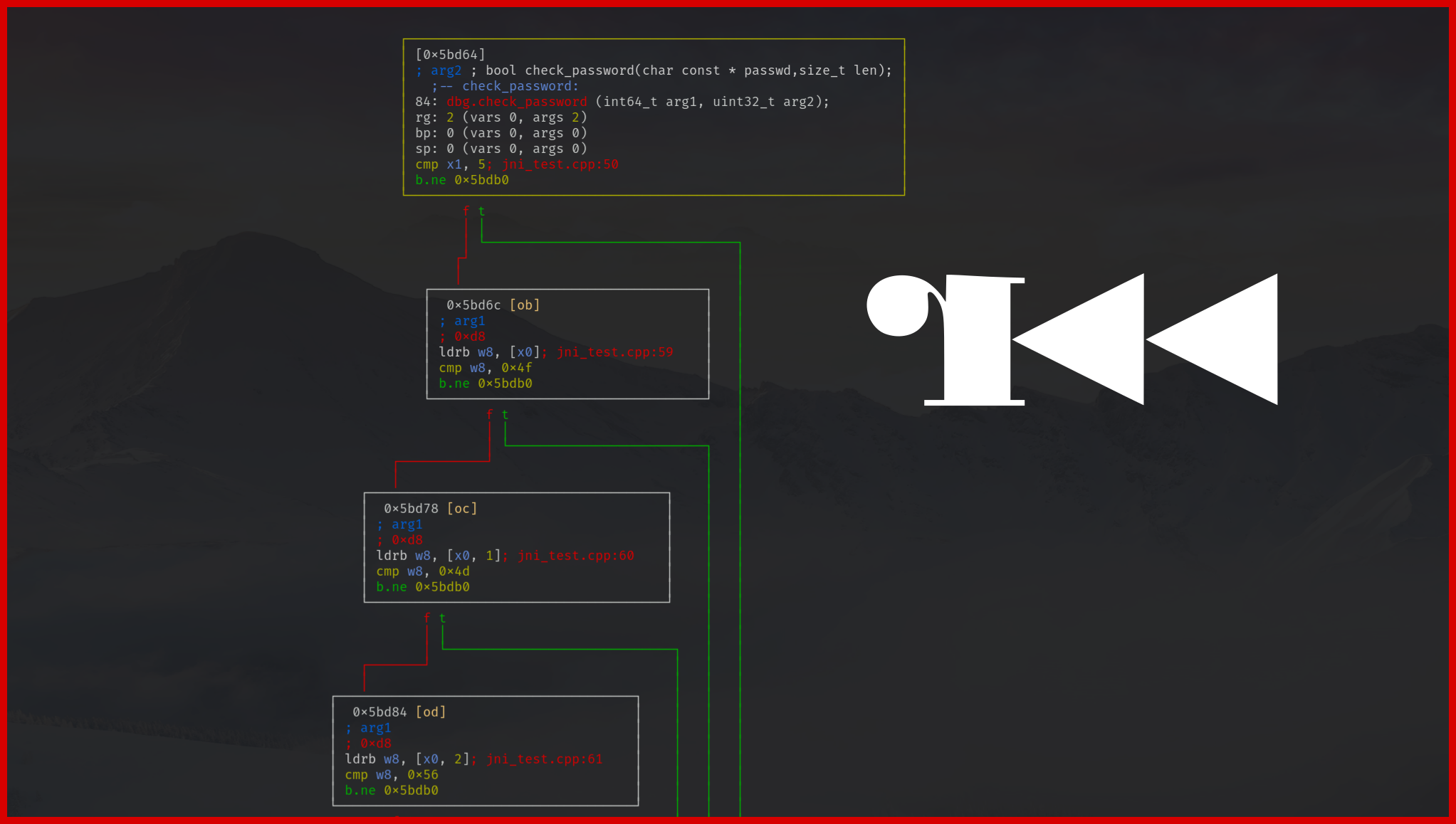
From this previous code, we could – with some effort – recover the semantic of the original function but when a reverse engineer has to deal with this protection on a large function, it’s a static pain. In the following slider, you can observe the effect of this pass on the control-flow graph:

Consequently, if the overall logic of the function is sensitive, you should enable this pass.

How to use it?

In the O-MVLL configuration file, you must define the following method in the Python class implementing omvll.ObfuscationConfig:

def flatten_cfg(self, mod: omvll.Module, func: omvll.Function):
    if func.name == "check_password":
        return True
    return False

Implementation

This pass was already present in the original O-LLVM project (Obfuscation/Flattening.cpp), but we did some improvements.

First, the next state to execute is determined by a random identifier (like in O-LLVM) but also by an encoding function. In the original implementation of O-LLVM, we have this kind of transformation:

switch (state) {
  case 0xedf34: state = 0x48179;
  case 0x48179: state = ...;
}

In the O-MVLL implementation, we added an encoding on the state variable:

switch (Encoding(state)) {
  case 0xedf34: state = 0xaaaa;
  case 0x48179: state = ...;
}

This additional encoding is used to hinder a static identification of the next states of a basic block. It also hinders attacks which would consist in tracing the memory writes accesses on the state variable. This encoding is not a very strong additional protection but it introduces overhead for the reverse engineer .

Second enhancement, the default basic block of the switch case is filled with corrupted assembly instructions:

auto* defaultCase = BasicBlock::Create(F.getContext(),
                                       "DefaultCase", &F, flatLoopEnd);
...
Value* rawAsm = InlineAsm::get(
  FType,
  R"delim(
  ldr x1, #-8;
  blr x1;
  mov x0, x1;
  .byte 0xF1, 0xFF;
  .byte 0xF2, 0xA2;
  )delim",
  "",
  /* hasSideEffects */ true,
  /* isStackAligned */ true
);
DefaultCaseIR.CreateCall(FType, rawAsm);
DefaultCaseIR.CreateBr(flatLoopEnd);

This stub is the reason why IDA fails to represent the graph of the function being flattened.

The default case of the switch should not be reached as all the states should be covered by the pass (or there is a bug). Thus, we can leverage this basic block to put instructions that are confusing for the disassemblers.

Limitations

This pass modifies the sequence of the basic blocks to hinder the overall structure of the function, BUT it does not protect the code of the individual basic blocks.

This means that a reverse engineer can still analyze the function at a basic block level to potentially extract the original logic. That’s why the basic blocks need to be protected with other obfuscation passes like String Encoding, Opaque Fields Access, Arithmetic Obfuscation.

In the current implementation, the encoding function is linear and does not change:

$$E(S) = (S \oplus A) + B$$

Nevertheless, $A$ and $B$ are randomly selected for each function.

References